 Abstraction faite des mesures, ces grandeurs physiques d’intérêt sont obtenues en exécutant un calcul de neutronique dénommé « calcul de cœur ». Leur connaissance permet alors d’accéder aux paramètres clés de sûreté, à savoir les facteurs de point chaud correspondant aux pics de puissance dans le cœur, les coefficients de réactivité qui traduisent la sensibilité de la réaction en chaîne à la variation de paramètres physiques tels que la température du combustible nucléaire et celle du modérateur, et la marge d’antiréactivité qui indique l’amplitude de la réduction de la réactivité du cœur (ou niveau de sous-criticité) du cœur lors d’un arrêt automatique du réacteur.
Abstraction faite des mesures, ces grandeurs physiques d’intérêt sont obtenues en exécutant un calcul de neutronique dénommé « calcul de cœur ». Leur connaissance permet alors d’accéder aux paramètres clés de sûreté, à savoir les facteurs de point chaud correspondant aux pics de puissance dans le cœur, les coefficients de réactivité qui traduisent la sensibilité de la réaction en chaîne à la variation de paramètres physiques tels que la température du combustible nucléaire et celle du modérateur, et la marge d’antiréactivité qui indique l’amplitude de la réduction de la réactivité du cœur (ou niveau de sous-criticité) du cœur lors d’un arrêt automatique du réacteur.
Échelles physiques impliquées en neutronique
Espace : 10-15 m : distance d’interaction neutron-noyau
; 10-3 à 10-1 m : libre parcours moyen des neutrons avant interaction ;
10-1 à 1 m : libre parcours moyen des neutrons avant absorption ; 1 à
plusieurs dizaines de mètres : dimension d’un réacteur nucléaire.
Temps
: 10-23 - 10-14 s : Interaction neutron-noyau ; 10-6 à 10-3s : temps de
vie des neutrons dans les réacteurs ; 10-2s : transitoire dans un
accident de criticité ; 10 s : retard à l’émission des neutrons retardés
; 100 s : transitoire dans une mise à l’équilibre thermique ; 1 jour :
transitoire dû au xénon 135 ; 1 à 4 ans : irradiation d’un combustible
nucléaire ; 50 ans : ordre de grandeur de la durée de vie d’une centrale
nucléaire : 300 ans : “extinction radioactive” des produits de fission
(quelques exceptions) ; 103 à 109 ans : nucléides à vie longue.
Énergie
: 20 MeV – 10-11 MeV (voire qq 10-13 MeV pour les neutrons
ultras-froids). Pour les systèmes à spallation* : quelques GeV à 10-11
MeV.
Les approches de modélisation et de simulation adoptées en neutronique sont en général de deux sortes, déterministe et probabiliste. Les données à mobiliser dans un calcul de cœur d’un réacteur nucléaire sont de différentes natures couvrant plusieurs échelles physiques (cf. encadré ci-dessus) :
- les données nucléaires (sections efficaces,…) qui caractérisent les interactions possibles entre un neutron et un noyau-cible ainsi que les sources de rayonnements qui en résultent,
- les données technologiques qui spécifient la forme, les dimensions, les compositions des différentes structures et composants du réacteur nucléaire,
- les données de fonctionnement du réacteur telles que l’historique de puissance,
- les données spécifiques aux méthodes numériques utilisées telles que les maillages spatiaux, énergétiques, angulaires, temporels relatifs à la modélisation déterministe ou bien le nombre de particules à simuler dans le calcul probabiliste.
Les calculs industriels requièrent de réduire drastiquement, par des modélisations appropriées, la dimension du problème à résoudre pour satisfaire un critère coût-précision exigeant (e.g. un calcul de cœur en quelques secondes).
Les calculs dits de ‟référence“ ou encore ‟High Fidelity“, quant à eux, veulent être les plus exhaustifs possible afin d’obtenir la variété et la finesse recherchées des résultats de calcul, ce qui peut représenter plusieurs centaines de millions de valeurs.
Dans les deux cas, les solveurs de calcul ont besoin d’être alimentés en amont par un très important volume de données nucléaires. Si l’on se place du point de vue de la masse de données à stocker et à traiter en regard des ressources informatiques disponibles pour ce faire, la problématique des données massives, vue sous cet angle, n’est pas entièrement nouvelle en neutronique. C’est l’objectif de la réalisation de calculs très fins de neutronique, devant mobiliser un volume de données nucléaires pouvant alors atteindre plusieurs Tera octets (1012 octets), qui conduit à repenser les codes de neutroniques à la fois pour exploiter pleinement les nouvelles opportunités matérielles offertes par les ressources du HPC*, tout en tenant compte aussi de leurs contraintes telles que celle, de prime abord paradoxale, de la diminution de la mémoire par thread* de calcul.
Bien entendu, la problématique des données massives va bien au-delà de l’aspect du stockage et du traitement des données d’entrée de solveurs de calcul. Récemment, avec l’avènement du Big Data et plus largement l’éclosion et le développement des Data sciences, il s’est opéré un renversement de la perspective épistémologique dans la manière de mener la recherche. Le Big Data offre la capacité d’« extraire des connaissances scientifiques à partir des données » et d’opérer des choix techniques à partir de la masse d’informations produites par de multiples simulations numériques. Ici, dans le domaine de la neutronique, notre préoccupation est de traiter les résultats provenant d’un nombre élevé de simulations numériques dans le but d’optimiser, simultanément sous plusieurs critères et contraintes, la configuration et les performances associées d’un cœur de réacteur nucléaire à eau sous pression (REP). L’exigence en puissance de calcul est alors supérieure, de plusieurs ordres de grandeur, à celle d’un calcul neutronique d’un cœur. Ainsi s’impose la nécessité de développer une stratégie efficiente d’optimisation.
Stratégie efficiente d’optimisation des cœurs de réacteur
Dans le domaine de l’optimisation, les algorithmes dits “évolutionnaires” ont commencé à être utilisés dans les années 1960 et 1970 avec l’accessibilité à des machines de calcul suffisamment puissantes.
Plusieurs approches ont été étudiées indépendamment, les plus connues étant les algorithmes génétiques, inspirés du vivant et de la modélisation des phénomènes s’y rapportant. Ils en empruntent également le vocabulaire. Le terme fédérateur d'algorithme évolutionnaire apparaît dans les années 1990, conjointement à un rapprochement des différentes communautés. C'est dans ces mêmes années que débute leur utilisation pour traiter des problèmes d'optimisation multi-objectifs ou multicritères.
Les algorithmes évolutionnaires sont des algorithmes à population. Chaque individu de la population représente une solution potentielle. La population évolue avec l'apparition et la disparition d'individus par phase successive appelée génération. Ainsi, ici, un réacteur nucléaire est assimilé à un individu caractérisé par son “génotype” et son “phénotype” tel qu’illustré sur la figure ci-dessous.
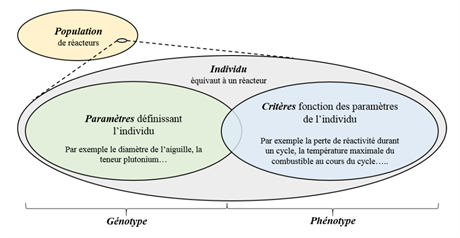
Caractérisation de configurations réacteur selon une approche génétique. © CEA
Dans son principe, le processus d’optimisation consiste à :
- générer au hasard un ensemble de N individus, nommés population initiale dans l’espace d’optimisation ;
- éliminer les individus ne respectant pas un ensemble de contraintes fixées ;
- classer les individus en fonction du degré de satisfaction des critères retenus (le “rang” au sens de Pareto) ;
- créer une nouvelle population par sélection, croisement et mutation ;
- évaluer la nouvelle population produite vis-à-vis des critères fixés.
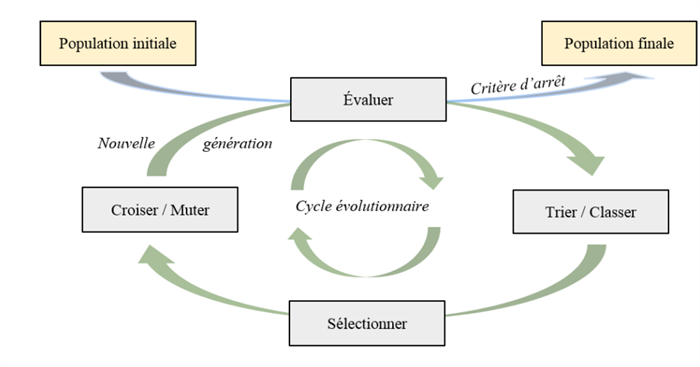
Algorithme évolutionnaire © CEA
Ces types d’algorithmes sont généralement utilisés lorsque les algorithmes classiques font défaut (problème ayant des discontinuités, non dérivable, présence de nombreux minimums locaux, problème mixte alliant variables continues et discrètes). Ils sont robustes et flexibles, mais nécessitent un nombre d'évaluations important, qui peut être atténué par leur parallélisme intrinsèque.
Il convient également de préciser que lorsque l’on procède à une optimisation multicritères (ou multi-objectifs) le résultat ne se résume pas à un seul individu (une seule configuration réacteur) mais à une population d’individus (un ensemble de configurations réacteur) appelée “Population Pareto optimale” et occupant dans l’espace des critères une région dénommée “Front de Pareto” dont des exemples sont donnés dans la suite.
Application à l’optimisation du rechargement du combustible
L’optimisation du rechargement du combustible dans les REP fait partie des problèmes de permutation pour lesquels l’objectif est de trouver parmi une liste d’éléments, un ordre particulier minimisant un critère donné.
L’exemple type est celui du voyageur de commerce devant passer par un ensemble de villes en minimisant la distance parcourue. C’est un problème NP-complet car le temps d’exécution de la résolution est exponentiel en fonction du nombre de villes. L’application présentée porte sur l’optimisation bi-objectifs du rechargement des assemblages combustibles d’un EPR sur les critères puissance locale et effet de vidange. À noter que par rapport aux premiers REP, l’optimisation du rechargement des EPR est plus complexe du fait des contraintes, des critères de sûreté, de l’hétérogénéité des assemblages et du manque de retours d’expérience.
Pour le résoudre nous avons utilisé un algorithme génétique [1] distribué qui fait évoluer plusieurs populations d’individus (plans de rechargement) de taille différente organisés en îlots. Ces îlots, au fonctionnement asynchrone adapté au HPC, favorisent par leur autonomie l’exploration de l’espace de recherche et par migrations d’individus entre îlots un enrichissement mutuel. Un croisement dédié a été utilisé intégrant des connaissances du problème : équivalence (inutile de permuter des assemblages équivalents neufs), similarité (les assemblages de même type et de même nombre de tours) ou des contraintes (positions ne pouvant accueillir certains assemblages). Le repositionnement du combustible est traité comme un problème multi-objectifs − pic de puissance, effet de vidange − avec des contraintes de sécurité portant sur les critères.
Les calculs numériques ont été réalisés à l’aide d’APOLLO3®, code de calcul multi-filière de physique des réacteurs sur le calculateur TITANE installé au CCRT du site CEA de Bruyères-le-Châtel (Centre de Calcul Recherche et Technologie, une des composantes du Très Grand Centre de calcul du CEA à
Bruyères-le-Châtel). Les calculs APOLLO3® ont été pilotés par la librairie VIZIR [5] intégrée à la plateforme logicielle URANIE [6] qui offre diverses méta-heuristiques d’optimisation mono et multicritères.
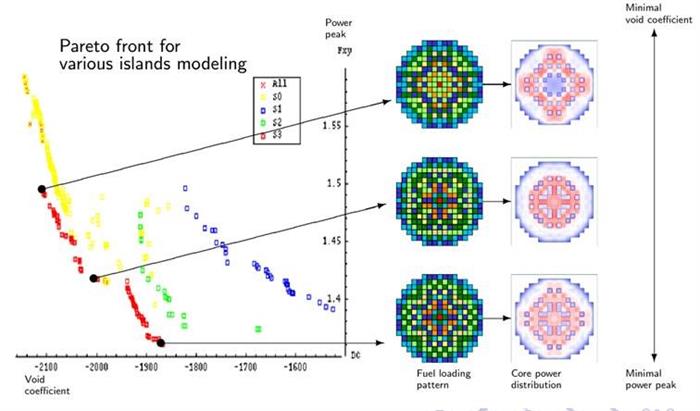
Dans le plan {puissance locale coefficient de vide}, les fronts de Pareto obtenus par 3 stratégies différentes d’îlots. © CEA
Différentes simulations ont été effectuées avec des îlots homogènes et hétérogènes qui, pour calculer le premier critère, utilisent une modélisation du cœur respectivement 2D ou 2D et 3D [1]. La Figure 4 montre les fronts de Pareto obtenus avec ces différents types d’îlots pour l'optimisation du pic de puissance et de l'effet de vidange. Les meilleures solutions (en rouge) ont été obtenues avec la stratégie par îlots hétérogène2D/3D où les îlots 2D, qui évoluent plus rapidement, permettent aux îlots 3D, plus lents, d’être réactualisés périodiquement avec de potentiels « bons individus ».
Dans [2], on a utilisé également cette stratégie d’algorithmes évolutionnaires distribués pour mener une optimisation bi-objectifs (puissance locale, effet de vidange) des hétérogénéités radiales et axiales dans un grand cœur de REP. Dans cet exercice, on a distribué sur les îlots, différents types d’algorithmes évolutionnaires, génétiques, colonies de fourmis, essaims particulaires tout en conservant la même modélisation pour l’évaluation des critères. Enfin, dans [3,4], ces algorithmes ont été utilisés pour la conception de nouveaux cœurs RNR-Na ainsi que le montre l’exemple d’application ci-après.
Application à la conception du réacteur ASTRID
La conception d’un réacteur nucléaire conduit à explorer un nombre conséquent de configurations possibles, chacune soumise à une série de critères et de contraintes. Prenons le cas du prototype de réacteur ASTRID - Advanced Sodium Technological Reactor for Industrial Demonstration - de 4e génération, d’une puissance de 600 MWe qui doit répondre aux contraintes environnementales et démontrer sa viabilité industrielle en satisfaisant à un niveau de sûreté au moins équivalent aux réacteurs de troisième génération, en intégrant le retour d’expérience de l’accident nucléaire de Fukushima, en envisageant la transmutation des actinides mineurs [3].
Pour ce réacteur les critères à minimiser sont la variation en réactivité en fin de cycle, le coefficient de vidange, la température maximale du sodium durant une séquence accidentelle ULOF, un critère économique lié à la masse du combustible nucléaire et au volume du cœur. Les contraintes à respecter sont la variation maximale de la réactivité sur un cycle (2600 pcm*), la fourchette du gain de régénération (-0,1 - +0,1), le nombre maximal de dpa* (140), le volume maximal du cœur (13,7 m3), la température maximale du sodium durant une séquence accidentelle ULOF (1200°C), la température maximale du combustible en fin de cycle (2500°C).
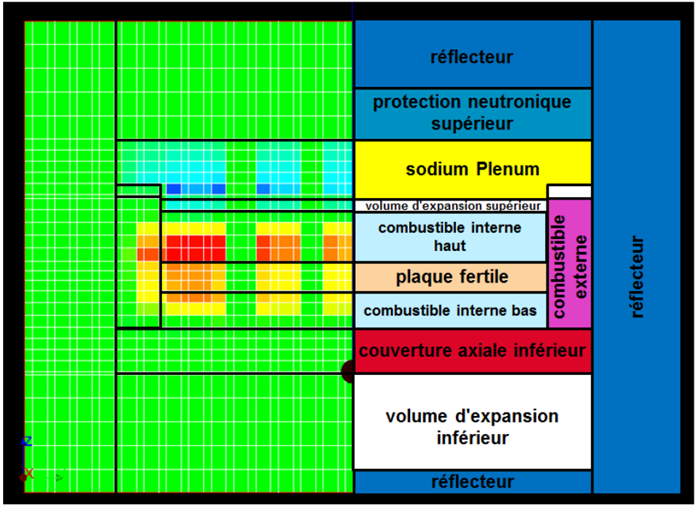
À droite, visualisation simplifiée du cœur ASTRID ; à gauche, décomposition spatiale de l’effet de dilatation du sodium sur la réactivité d’ASTRID : les zones rouges augmentent la réactivité du cœur, les zones bleues la diminuent. © CEA
Pour réaliser cette étude les performances de plus de dix millions de réacteurs ont été évaluées afin de pouvoir sélectionner les configurations de réacteurs optimales vis-à-vis des critères et contraintes fixés. L’exploration dans l’espace de recherche s’est faite par l’intermédiaire de méta-modèles (réseaux de neurones par exemple) pour réduire les temps de calcul.
Vue du prototype de réacteur Astrid © CEA/P. Stroppa
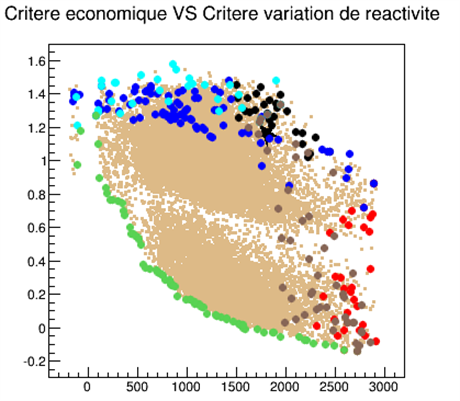
Exemple d’un front de Pareto (points verts) obtenu pour deux critères : critère économique versus critère de variation de la réactivité.
© CEA
Ainsi, cette méthode appliquée aux études de conception d’ASTRID a abouti à la caractérisation d’une « Population Pareto optimale » (c.à.d. impossible d’améliorer un critère sans contrepartie pénalisant les autres critères) de 25 000 individus-réacteurs. Elle a fourni des résultats tels que ceux illustrés sur la figure ci-après via une visualisation en coordonnées parallèles (aussi nommée COBWEB) où chaque fil correspond à un individu (un réacteur), chaque barre représente la plage de variation au sein de la population, des caractéristiques (critères, paramètres, propriétés) reflétant les critères-performances des réacteurs, retenus plus haut.
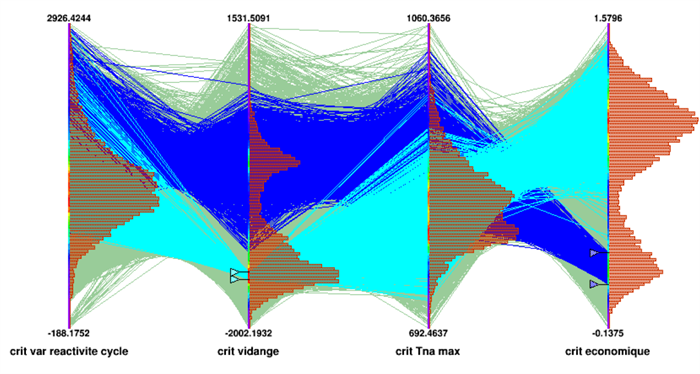
Répartition statistique des critères sur le front de Pareto. On peut constater que les cœurs performants sur le critère portant sur la vidange (cœurs en bleu-clair) peuvent aussi être performants sur le critère portant sur la variation de réactivité et la température maximale du sodium (Tna Max). Ils sont cependant médiocres sur le critère économique. L’inverse est aussi vrai (cœurs en bleu-foncé)
.
© CEA
Ces études ont montré l’intérêt des algorithmes évolutionnaires exécutés en HPC pour résoudre des problèmes complexes d’optimisation multicritères sous contraintes. Aujourd’hui, les moyens de calcul HPC permettent d’utiliser des méta-heuristiques, d’exploiter naturellement le parallélisme des moyens de calcul et enfin de combiner différentes stratégies de recherche. L’ensemble de ces travaux ont attiré l’attention sur des améliorations possibles pour traiter de ce qu'on appelle le “many-objectives”, lorsque le nombre d'objectifs est élevé. D'autres domaines de recherche sont ouverts, notamment l'optimisation sous incertitudes, qu'il s'agisse d'incertitudes aléatoires* ou/et épistémiques*.