Visible matter constitutes only 16% of the Universe's total mass. Little is known about the nature of the rest of that mass, which referred to as dark matter. Even more surprising is the fact that the Universe's total mass accounts for only 30% of its energy. The rest is dark energy, which is totally unknown but is responsible for the Universe's accelerated expansion.
To find out more about dark matter and dark energy, astrophysicists use large-scale surveys of the Universe or detailed studies of the properties of galaxies. But they can only interpret their observations by comparing them to predictions by theoretical models of dark matter and dark energy. But these simulations take tens of millions of computing hours on supercomputers.
The Extreme-Horizon collaboration was able to run a simulation of the evolution of cosmic structures from the first few moments after the Big Bang to the present day, on the Joliot-Curie supercomputer, which offers computing power of 22 petaflops (22 x 1015 floating point operations per second). The volume of numerical data processed exceeded 3 TB (1012 bytes) at each step of the computation, justifying the use of new techniques for writing (RAMSES code with adaptive mesh refinement) and reading the simulation data.
Cosmology: correcting the data from the Lyman-α forest
The simulation's first result concerns the interpretation of large structures of the distant Universe: intergalactic hydrogen clouds. Astrophysicists detect these by measuring the absorption of light from quasars, which are extremely luminous due to the presence of a supermassive black hole that attracts matter in its accretion disk. Each of the clouds along the line of sight produces an 'absorption line' (Lyman-α) with a specific redshift, due to the expansion of the Universe. All these lines form a dense 'forest', revealing the one-dimensional distribution of the hydrogen clouds, and therefore of matter, at distances between 10 and 12 billion light-years (ly).
However, many black holes between these quasars and us expel a considerable amount of energy into the intergalactic medium, changing its thermal state and the properties of the Lyman-α forest. The physical model used in the Extreme-Horizon simulation describes in detail this feedback, which biases estimates of cosmological parameters by several percent. The correction factor calculated will be vital, particularly for the DESI (Dark Energy Spectroscopic Instrument) experiment under construction in Arizona (USA), because the bias can exceed 5%, whereas the target accuracy is 1%.
Ultra-compact massive galaxies formed like a 'beehive'
The Extreme-Horizon simulation's high resolution in low density regions meant that it was able to describe 'cold' gas accretion by galaxies and the formation of ultra-compact massive galaxies when the Universe was only 2 to 3 billion years old. These atypical galaxies, recently observed with the Alma (Atacama Large Millimeter/Submillimeter Array) radiotelescope in Chile, are formed by the rapid clustering of many very small galaxies. It was only possible to identify this 'beehive' method of growth because of Extreme-Horizon's exceptional resolution.
Grand challenge on the Joliot-Curie supercomputer
Designed by the company Atos for GENCI (the French high-performance computing centre), the Joliot-Curie supercomputer, based on Atos's BullSequana architecture, reached a peak computing power of 22 petaflops in 2020.
Grand challenges are exceptional simulations and computations carried out during the 'Grand Challenge' period which follows the installation of a new computer partition. This three-month period provides a unique opportunity for a small number of users to access a large share of the machine's resources. They benefit from the support of the TGCC's and the manufacturer's teams, working together to optimize the computer's operation during this 'startup' phase.
Extreme-Horizon was run on the new AMD ROME computation partition of GENCI's Joliot-Curie supercomputer, operated by teams of computer scientists from the CEA's Military Applications Division (DAM) at the Very Large Computing Centre (TGCC at Bruyères-Le-Châtel). The simulation took fifty million computing hours and used new data reading and writing techniques to reduce the disk space used and accelerate data access. The work was done with the support of several institutes and divisions within the CEA and of Université Paris-Saclay's High-Performance Computing and Simulation Laboratory
The project was run as a collaboration between CEA-Irfu, AIM (CEA, CNRS, Université de Paris), IAP (CNRS, Sorbonne Université) and LIHPC (Université Paris-Saclay, CEA-DAM).
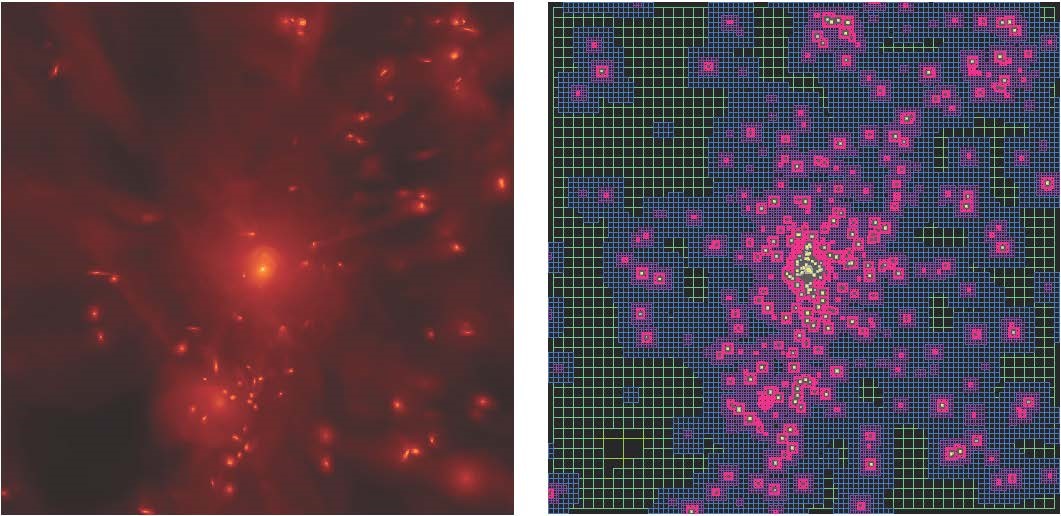
The RAMSES simulation code is a numerical code for astrophysics and cosmology. It is based on an adaptive mesh refinement computing technique. The figure illustrates the adaptive mesh configuration based on the density of matter.

Figure 1. View of the Extreme-Horizon simulation. The red is hot gas, generally expelled from galaxies by supermassive black holes. The grey is primordial cold gas, which feeds the galaxies along the cosmic filaments. The green is gas enriched with heavy elements (metals) due to the effect of massive star explosions (supernovae)
 Figure 2. View of the Extreme-Horizon simulation showing a region of 50 Mpc square. The gas temperature is shown here (violet ~10^4K - yellow ~10^7K). The main galaxies appear as cold spots within vast haloes of hot gas
Figure 2. View of the Extreme-Horizon simulation showing a region of 50 Mpc square. The gas temperature is shown here (violet ~10^4K - yellow ~10^7K). The main galaxies appear as cold spots within vast haloes of hot gas
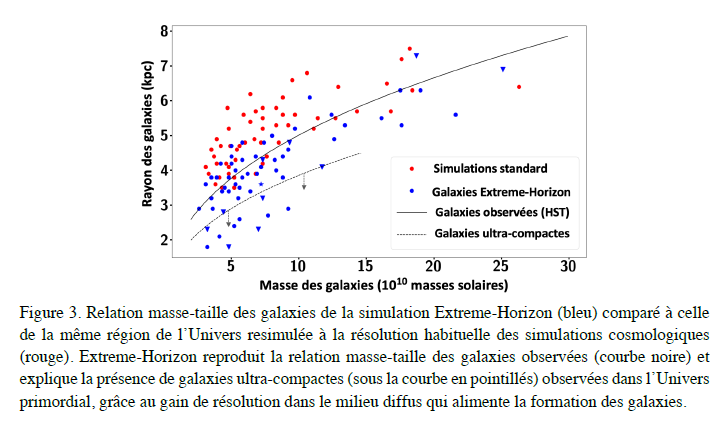
Figure 3. Mass-to-size ratio of the galaxies in the
Extreme-Horizon simulation (blue) compared to the ratio for the same region of
the Universe re-simulated at the normal resolution of cosmological simulations
(red). Extreme-Horizon reproduces the mass-to-size ratio of the galaxies
observed (black curve) and explains the presence of ultra-compact galaxies
(under the dashed curve) observed in the primordial Universe, through improved
resolution in the diffuse medium that feeds galaxy formation.

Mass-to-size ratio of the galaxies in the Extreme-Horizon simulation (blue) compared to the ratio for the same region of the Universe re-simulated at the normal resolution of cosmological simulations (red). Extreme-Horizon reproduces the mass-to-size ratio of the galaxies observed (black curve) and explains the presence of ultra-compact galaxies (under the dashed curve) observed in the primordial Universe, through improved resolution in the diffuse medium that feeds galaxy formation. Starbursts in and out of the star-formation main sequence - Elbaz, D.; Leiton, R.; Nagar, N.; Okumura, K.; et al. A&A 616, A110 (2018)