Quite apart from measurements, these physical parameters of interest are obtained by running a neutronics calculation called the “core calculation”. Once they have been obtained, it is then possible to access key safety parameters, that is the hot spot factors corresponding to the power peaks in the core, the reactivity coefficients which reflect the sensitivity of the chain reaction to the variation in physical parameters such as the temperature of the nuclear fuel and that of the moderator, and the anti-reactivity margin which indicates the amplitude of the reduction in core reactivity (or subcriticality level) during a reactor scram.
Physical scales used in neutronics
- Space: 10-15 m: neutron-nucleus interaction distance; 10-3 to 10-1 m: average free neutron path before interaction; 10-1 to 1 m: average free neutron path before absorption; 1 to several tens of metres: dimension of a nuclear reactor.
- Time: 10-23 - 10-14 s: Neutron-nucleus interaction; 10-6 to 10-3s : lifespan of neutrons in reactors; 10-2s: transient in a criticality accident; 10 s: delay in emission of delayed neutrons; 100 s: transient in achieving thermal equilibrium; 1 day: transient due to xenon 135; 1 to 4 years: irradiation of a nuclear fuel; 50 years: approximate lifetime of a nuclear power plant: 300 years: “radiation extinction” of fission products (a few exceptions); 103 to 109 years: long-lived nuclides.
- Energy: 20 MeV – 10-11 MeV (or even a few 10-13 MeV for ultracold neutrons). For spallation systems*: a few GeV to 10-11 MeV.
There are generally two types of modelling and simulation approaches used in neutronics: deterministic and probabilistic. The data to be used in a nuclear reactor core calculation are of different types and cover several physical scales (see box above):
- nuclear data (cross-sections, etc.) characterising the possible interactions between a neutron and a target nucleus, as well as the resulting sources of radiation,
- technological data specifying the shape, dimensions, compositions of the various structures and components of the nuclear reactor,
- the reactor operating data and power history,
- the data specific to the numerical methods used, such as the spatial, energy, angular, time meshes for deterministic modelling, or the number of particles to be simulated in a probabilistic calculation.
Industrial calculations require the use of appropriate modelling to achieve a drastic reduction in the dimension of the problem to be resolved, to meet a demanding cost-precision criterion (for example, a core calculation in a few seconds).
“Benchmark” or ‟High Fidelity“ calculations for their part aim to be as exhaustive as possible in order to obtain the required variety and detail in the calculation results, which can represent several hundred million values.
In both cases, the calculation solvers need to be supplied upstream by a very large volume of nuclear data. From the standpoint of the mass of data to be stored and processed given the available computing resources, the problem of massive data is not exactly a new one for neutronics. It is the goal of carrying out extremely detailed neutronics calculations, utilising a volume of nuclear data that can reach several terabytes (1012 bytes), which means that we must take a fresh look at neutronics codes, both to take full advantage of the opportunities offered by HPC* resources, while also taking account of their constraints, above all such as the seemingly paradoxical reduction in memory by core* computing.
Of course the problem of massive data goes well beyond the storage and processing of calculation solver input data. Recently, with the advent of Big Data and more generally the emergence and growth of the data sciences, a complete turnaround took place in the epistemological perspective on how to carry out research. Big Data offers the ability “extract scientific knowledge from data” and to make technical choices from the mass of information produced by multiple numerical simulations. Here, in the field of neutronics, our concern is to process the results from a large number of numerical simulations, in order to optimise the configuration and corresponding performance of a pressurised water reactor (PWR) nuclear reactor core, simultaneously with several criteria and constraints. The computing power requirement is then several orders of magnitude greater than that of a neutronics core calculation. There is thus the need to develop an efficient optimisation strategy.
Reactor core efficient optimisation strategy
In the field of optimisation, evolutionary algorithms have been used since the 1960s and 1970s when sufficiently powerful computers became available.
Several approaches were studied independently, the best-known being genetic algorithms, inspired by the life sciences and the modelling of the relevant phenomena. They also use the same vocabulary. The umbrella term evolutionary algorithm appeared in the 1990s, jointly with a merging of various communities. They began to be used at the same time to deal with multi-objective or multi-criteria optimisation problems.
Evolutionary algorithms are population-based algorithms. Each individual in the population represents a potential solution. The population evolves with the appearance and disappearance of individuals in successive phases, called generations. Thus a nuclear reactor is here compared to an individual characterised by his “genotype” and his “phenotype” as illustrated in the following figure.
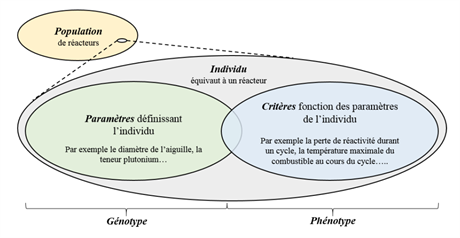
Characterisation of reactor configurations using a genetic approach. © CEA
In principle, the optimisation process consists in:
- randomly generating a set of N individuals, called the initial population in the optimisation space;
- eliminating individuals who do not meet a set of fixed constraints;
- classifying the individuals according to the degree to which the selected criteria are met (the “ranking” as defined by Pareto);
- creating a new population by selection, recombination and mutation;
- evaluating the new population produced against the defined criteria.
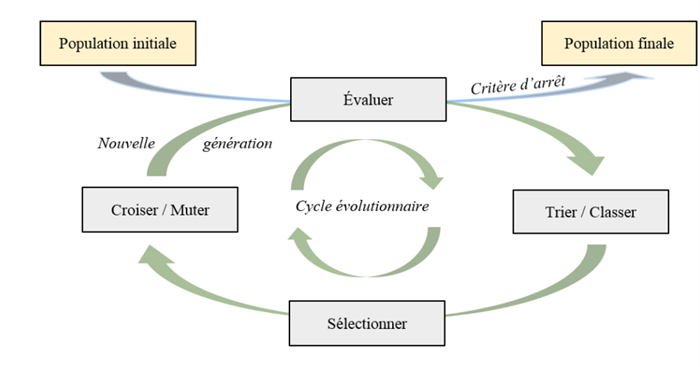
Evolutionary algorithm © CEA
These types of algorithms are generally used when conventional algorithms are not up to the job (problem with discontinuities, non-derivable, presence of numerous local minimums, mixed problem involving continuous and discrete variables). They are robust and flexible, but require a large number of evaluations, which can be attenuated by their intrinsic parallelism.
It should also be pointed out the when a multi-criteria (or multi-objective) optimisation is carried out, the result is not just about a single individual (or a single reactor configuration) but a population of individuals (a set of reactor configurations) called the “Optimal Pareto Population” and occupying a region in the criteria space called the “Pareto Front” examples of which are given below.
Application to optimisation of fuel reloading
The optimisation of fuel reloading in PWRs is among the permutation problems for which the aim is to find a particular order among a list of elements, minimising a given criterion.
The typical example is that of a commercial traveller who has to pass through a set of towns, while minimising the distance travelled. This is an NP-complete problem because the resolution execution time is exponential to the number of towns. The application presented concerns the twin-objectives optimisation of reloading PWR fuel assemblies according to the local power and void effect criteria. It should be noted that by comparison with the first PWRs, the optimisation of EPR refuelling is more complex owing to the constraints, the safety criteria, the heterogeneous assemblies and the lack of operating experience feedback.
To resolve it, we used a distributed genetic algorithm [1] which triggers the evolution of several populations of individuals (refuelling plans) of different sizes organised into islands. The independence of these islands, with asynchronous operation suited to HPC, favours the exploration of the research space as well as mutual enrichment by migration of individuals between islands. A dedicated combination was used, integrating knowledge of the problem: equivalence (pointless to switch equivalent new assemblies), similarity (assemblies of the same type and the same number of cycles) or constraints (positions which cannot accept certain assemblies). The repositioning of the fuel is dealt with as a multi-objective problem – power peak, void effect – with safety constraints relating to the criteria.
The numerical calculations were performed using APOLLO3®, a multi-purpose computing code for reactor physics on the TITANE computer installed in the CCRT on CEA’s Bruyères-le-Châtel site. The APOLLO3® calculations were driven by the VIZIR library [5] integrated into the URANIE [6] software platform, which offers various single and multi-criteria optimisation meta-heuristics.
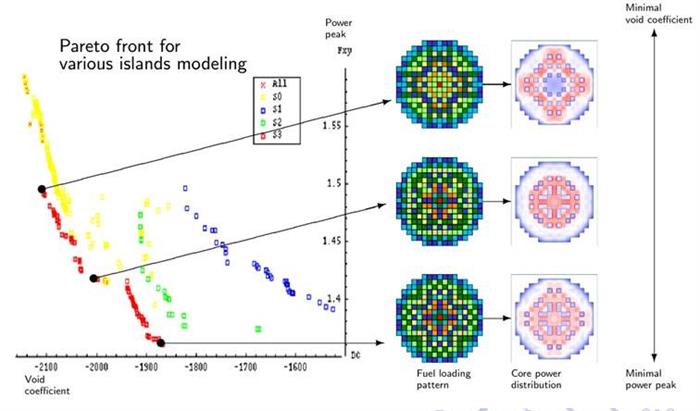
In the plane {local power void coefficient}, the Pareto fronts obtained by 3 different island strategies. © CEA
Different simulations were carried out with homogeneous and heterogeneous islands which, in order to calculate the first criterion, use 2D or 2D and 3D core modelling respectively [1]. Figure 4 shows the Pareto fronts obtained with these different types of islands, for optimisation of the power peak and the void effect. The best solutions (in red) were obtained with the strategy using 2D/3D heterogeneous islands or 2D islands, which evolve faster, enabling the slower 3D islands to be periodically updated with potential “good individuals”.
In [2], we also used this distributed evolutionary algorithms strategy to run a dual-objectives optimisation (local power, void effect) of the radial and axial heterogeneities in a large PWR core. In this exercise, we distributed different types of evolutionary algorithms on the islands; genetic, ant colonies, particle swarms, while retaining the same modelling for evaluation of the criteria. Finally, in [3,4], these algorithms were used to design new FNR-Na cores as shown in the following application example.
Application to the design of the ASTRID reactor
The design of a nuclear reactor entails the exploration of a significant number of possible configurations, each subject to a series of criteria and constraints. Let us take the example of the prototype generation IV reactor, called ASTRID – Advanced Sodium Technological Reactor for Industrial Demonstration – with a power of 600 MWe and which must meet environmental constraints and demonstrate its industrial viability while meeting a level of safety at least equivalent to the third generation reactors, taking into account the lessons learned from the Fukushima nuclear accident and envisaging the transmutation of the minor actinides [3].
For this reactor, the criteria to be minimised are the variation in reactivity at the end of the cycle, the void coefficient, the maximum sodium temperature during an ULOF* accident sequence, an economic criterion linked to the mass of nuclear fuel and the volume of the core. The constraints to be met are the maximum variation in reactivity over a cycle (2600 pcm*), the regeneration gain range (-0.1 - +0.1), the maximum number of dpa* (140), the maximum core volume (13.7 m3), the maximum sodium temperature during an ULOF accident sequence (1200°C), the maximum fuel temperature at the end of the cycle (2500°C).
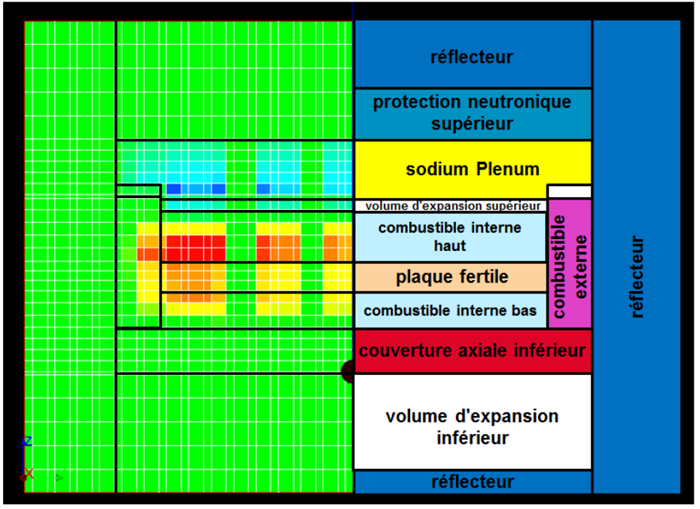
Right, simplified representation of the ASTRID code; left, spatial breakdown of the sodium expansion effect on the reactivity of ASTRID: the red zones increase core reactivity, the blue zones reduce it. © CEA
To carry out this study, the performance of more than ten million reactors was evaluated for selection of the optimum reactor configurations with respect to the criteria and constraints defined. Exploration in the research space is by means of meta-models (neural networks for example) to reduce the computing time.
The generation IV reactor technology demonstrator called ASTRID, currently at the design stage. © CEA/P. Stroppa
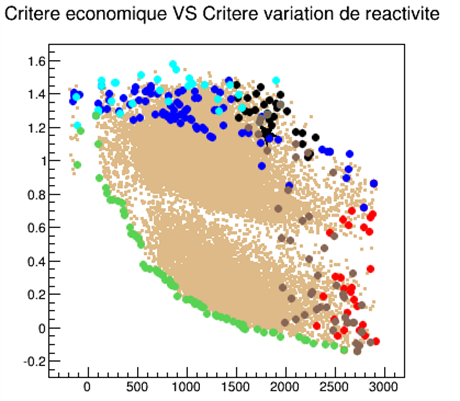
Example of a Pareto front (green dots) obtained for two criteria: economic criterion versus reactivity variation criterion.
© CEA
When applied to the ASTRID design studies, this method therefore led to the characterisation of an “optimal Pareto population” (in other words, impossible to improve one criterion without penalising the others) of 25,000 individuals-reactors. It gave results such as those illustrated in the following figure by means of a parallel coordinates visualisation (also called COBWEB) in which each line corresponds to an individual (a reactor) and each axis represents the variation range, within the population, of the characteristics (criteria, parameters, properties) reflecting the reactor performance criteria mentioned above.
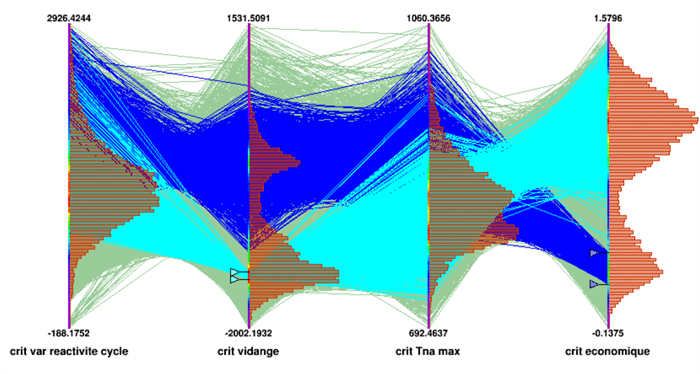
Statistical distribution of criteria on the Pareto front. It can be seen that the cores which perform well on the void criterion (light blue) may also perform well on the reactivity variation and maximum sodium temperature (Tna Max). They are however mediocre with respect to the economic criterion. The opposite is also true (dark blue cores).
© CEA
These studies showed the benefits of evolutionary algorithms run in HPC for resolving complex multi-criteria optimisation problems with constraints. HPC computing resources today enable meta-heuristics to be used, naturally making use of the parallelism of the computing means and finally combining various research strategies. These works as a whole drew attention to the possible improvements for processing what is referred to as “many-objectives”, when the number of objectives is high. Other fields of research have appeared, in particular optimisation under uncertainties, whether random or/and epistemic.