By default, TRIPOLI-4® uses common variance reduction techniques such as implicit capture, particle splitting and Russian roulette, so that particle transport is non-analog.
Moreover, TRIPOLI-4® has a special built-in variance reduction module called INIPOND. The key algorithm of INIPOND is based on the Exponential Transform method [1], with an automatic pre-calculation of the importance map. For shielding configurations associated to deep penetration problems, Tripoli-4® automatically pre-computes an importance map. This importance function is assumed to be factorized in space, energy, angle and time variables, with a coupling between space and energy variables. A space and energy grid has to be defined by the user for the initialization of the importance map by the code. An arbitrary of fictitious detectors (typically, one or a few) are actually placed by the user in the geometry and act as 'attractors' for simulated particles. These attractors are especially useful for dealing with passing-round configurations.
At the beginning of the simulation, adjustments of the importance map are performed from group to group by taking advantage of statistics on discrepancies between particle weights and reference weights given by the importance map, when particles slow down from group to group. If the Exponential Transform technique is used to perform non-analog flights, the sampling from the free flight kernel is performed by replacing the total cross-section by the biased macroscopic total cross-section, and statistical weights are adjusted accordingly.
Left to right: Reactor
Pressure Vessel flux assessment, display of collision sites with optimised variance reduction
In addition to producing an internally-generated importance map, Tripoli-4® is also capable of reading an external importance function produced by a deterministic code by solving the adjoint Boltzmann equation on a space and energy mesh. Successful tests have been performed by coupling the importance map generated by the deterministic code APOLLO3 to Tripoli-4® for shielding problems [2].
For coupled neutron-photon simulations, two importance maps may be required. For such configurations, a diagnosis tool is now available in Tripoli-4® so as to facilitate the adjustment of the neutron importance map [3].
During the simulation, the Exponential Transform method is also combined with a quota sampling algorithm and splitting and Russian roulette are finally performed before each track-length and collision sampling, according to the importance map.
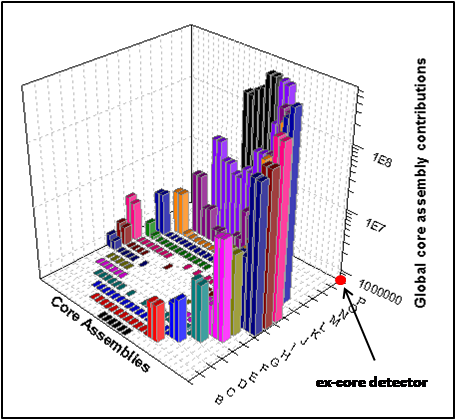
Ex-core chamber : example of source contribution calculation using Green’s functions.
Tripoli-4® allows for Green's functions calculations for parametric source analyses [4]. The algorithm is based on the pre-calculation of Green's functions between source and tally areas. The storage is performed during a first standard run generally based on the efficient variance reduction techniques of the code. Then, for any new source configuration, the requested tallies are computed by recombining the Green's function values with the new source distribution, without simulating any particle history. Fine source contribution analysis can also be achieved through this feature. Analyses can thus be performed in much shorter calculation times, when compared with full Monte Carlo simulations.
A new variance reduction method has been recently proposed in the literature of applied mathematics: the Adaptive Multilevel Splitting (AMS) [5]. Originally designed to help the simulation of rare events associated to continuous Markov chains, it has been extended to discrete Markov chains [6]. The AMS algorithm has been successfully transposed to the field of particle transport and implemented in TRIPOLI-4® as an effective variance reduction technique for neutron and photon transport [7], including coupled neutron-photon transport [8].
Recent additions to the capabilities of the code include the use of the CADIS (Consistent Adjoint-Driven Importance Sampling) method, using the adjoint flux computed by a deterministic solver as an importance map to preferentially sample the particles towards the detector region [9,10]. For TRIPOLI-4, the adoint flux is computed by the IDT solver of the deterministic APOLLO-3, developed at CEA [11]. In the IDT solver, spatial mesh cells are assumed to be homogeneous. In practice, a mesh cell can overlap with more than one volume of the TRIPOLI-4 model, with possibly different material compositions. IDT will assume that cells are filled with the material composition that is found at the center of the cell. IDT produces both neutron and photon importance maps; the development of the coupled neutron-photon adjoint solver is under way and will be provided in a future version of the code. The IDT solver is distributed with TRIPOLI-4; in addition, microscopic multi-group cross sections (in HDF format) are also distributed, for the sake of convenience: photon cross sections use a 94-group energy mesh, while the neutron cross sections use a 281-group energy mesh. The CADIS method has been successfully tested in combination with the legacy exponential transform method, based on international benchmarks and reference configurations (including cases where fissile media are also present, like in reactor start-up problems with ex-core detectors) [12, 13, 14, 15].
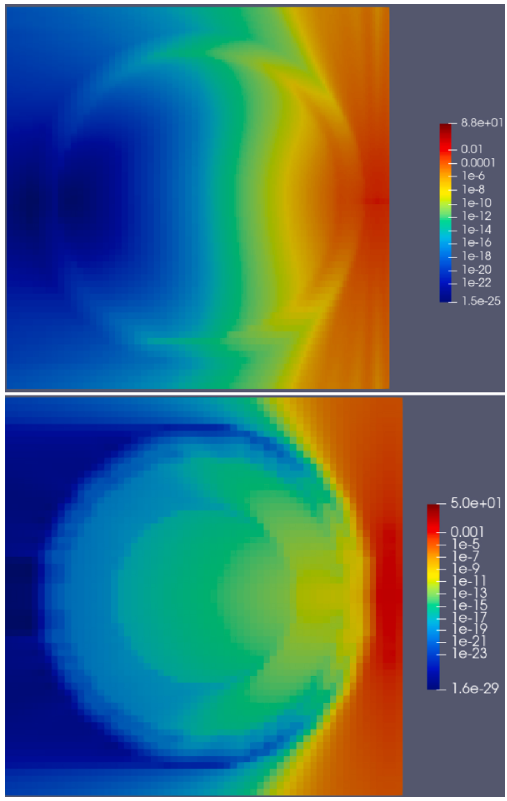
Neutron (top) and photon (bottom) spatial importance maps for a radiation shielding application: computing the reaction rate at a detector located in an out-of-vessel position. The detector position corresponds to the peak of the importance maps. The maps have been computed using the IDT solver to obtain the solutions of the adjoint neutron and photon problems on a spatial and energy mesh.
Furthermore, in TRIPOLI-4 we have also implemented the weight windows method, a variance-reduction strategy based on importance-driven splitting and Russian roulette that is currently used by several other Monte Carlo transport codes, such as MCNP [16]. This technique has shown great potential for solving radiation shielding problems, especially when the importance function required for the generation of the weight windows is obtained from the solution of the adjoint Boltzmann equation [15].