Together with average tallies, Tripoli-4 ® allows also for two perturbation schemes, namely
- the correlated sampling method and
- the Taylor series development (differential operator sampling).
The key idea behind the correlated sampling is the following [1]: let P be the law of the trajectories for the unperturbed simulation, and Pq the law corresponding to a transport process where the parameter q has been perturbed. In addition to the regular particle weight, we set a likelihood factor L(xi;q) = P(xi;q)=P(xi) that gives the relative probability of having a trajectory in state xi after transition i if it were simulated with probability Pq instead of P. Now, if we want to estimate the effect of a perturbation on a reaction rate or on any quantity of interest, whenever we increment the contribution to the unperturbed score by a quantity s, we have just to increment the perturbed score by an amount sL(xi;q). Then, if we want to estimate a differential effect, we increment the perturbed score by an amount of s(L(xi;q)-1).
In criticality simulation mode we also have to propagate the perturbation through generations so as to take into account the modification of the source distribution due to the perturbation. For the correlated sampling method, the parameters that can be perturbed are concentrations, densities and cross-sections.
The tallies that can be perturbed are fluxes, reaction rates and the multiplication factor.
Differential operator sampling [2] has been implemented in Tripoli-4® up to the second order in the Taylor expansion, including cross derivatives. Since the derivatives are calculated once for all, differential sampling is particularly suited for sensitivity analysis. Differential sampling is in good agreement with correlated sampling if cross derivatives are included in the Taylor expansion. Differential sampling allows perturbing concentrations and densities in fixed-source calculations.
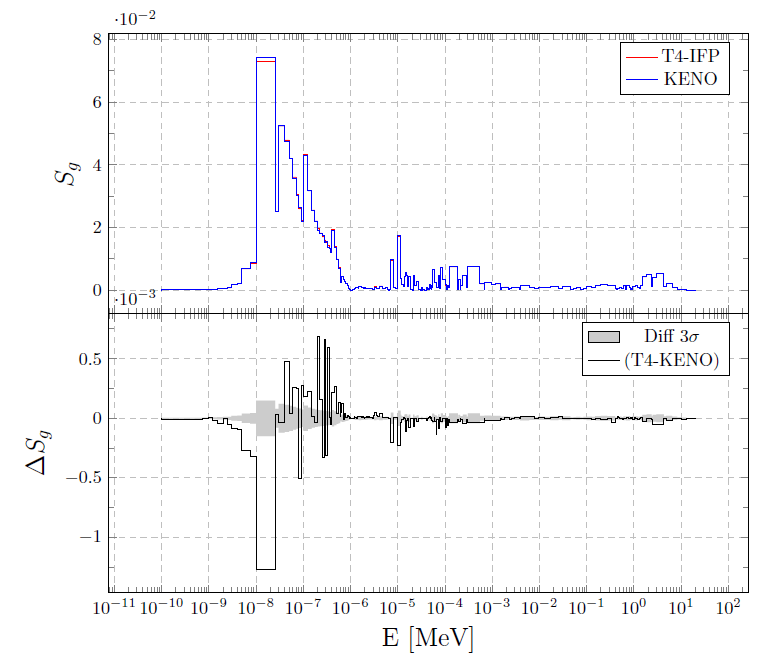
Computing the sensitivity of keff to fission neutron yield (MIX-COMP-THERM-001-001).
In addition to correlated sampling and differential operator sampling, Tripoli-4® can furthermore compute reactivity perturbations and sensitivities of the multiplication factor to nuclear data via the Iterated Fission Probability methods. Such methods are implemented via the reference calculation of the critical adjoint flux, which is used in order to weight the operator appearing in the bilinear forms required by the Standard Perturbation Theory [3].