Tripoli-4® can perform depletion calculations by coupling the code to the MENDEL depletion solver developed at CEA [1, 2]. This coupling is aimed at solving the Boltzmann-Bateman nonlinear set of equations that characterize the evolution of materials under neutron irradiation [3]. In order to solve the resulting nonlinear system, the total irradiation time is discretized into time steps.
The following procedure is then successively applied at each time step. First, Tripoli-4® computes the reaction rates in each depleted medium. Then, the depletion solver, which receives as an input these reaction rates, calculates the end-of-step concentration for each region. Tripoli-4® can either calculate global physical quantities such as the multiplication factor, the kinetics parameters, the burnup, and so on, or local quantities (i.e., for each depleted region) such as the power, reaction rates, nuclides concentrations, activities and masses.
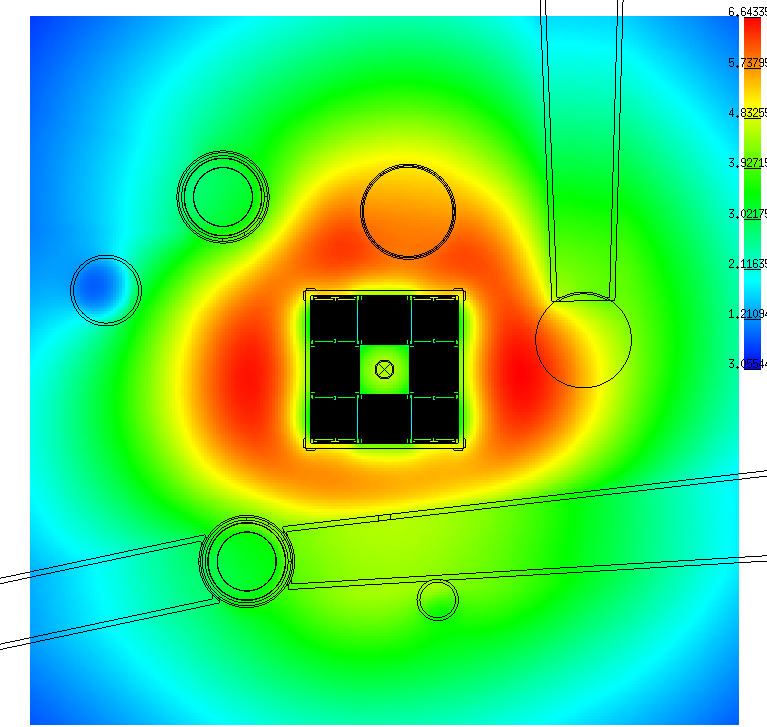
ORPHEE research reactor: three-dimensional core depletion analysis, radial thermal flux distribution.
Uncertainty propagation is a long-standing issue for Monte Carlo burnup codes. Indeed, the reaction rates given as an input to the deterministic depletion solver are random variables, and they thus induce uncertainties on isotopic inventories. In order to properly propagate these uncertainties through all the time steps, a full Monte Carlo approach has been adopted and made automatic in Tripoli-4®: it basically consists in running independent simulations [4, 5]. Post-processing tools are provided together with the code and allow the results to be easily recombined for the analyses. Confidence intervals for the desired physical quantities are computed as well.
Another issue affecting Monte Carlo burnup codes is the computation time, which is mainly due to the large number of tallies (especially the reaction rates), and to the hundreds of nuclides to be handled during the transport stage. In order to cope with the former case, multi-group reaction rates built from the fine multi-group flux and the corresponding GENDF cross-sections can be used. A list of nuclides to which this speed-up applies can be specified. In order to reduce the number of isotopes to be included for neutron transport, isotopic filters can be also used. These filters allow nuclides to be neglected for transport calculations, based on their respective contribution to fission or capture rates in each depleted medium.
To safely conduct maintenance operation or repair in a nuclear reactor (fission or fusion), the radiation dose map in the reactor building must be determined. These doses are due to the decay gamma emitted by the activated structures and the fuel in fission reactor. Two methods have been proposed to perform shut-down dose rate (SDR) calculations: the Rigorous Two-Steps (R2S) and the Direct One-Step (D1S) method [6]. The D1S scheme is based on a single coupled neutron-photon Monte Carlo transport calculation: prompt photons are replaced by decay photons. The R2S scheme is based on two Monte Carlo transport calculations, one for the neutrons in order to calculate the activation, and one for the photons emitted by activated materials.
In Tripoli-4®, activation calculations can be performed by resorting to the R2S approach [7], whose scheme is the following: first, Tripoli-4® performs a neutron transport calculation in order to compute the flux and/or the energy integrated reaction rates in each region susceptible to produce decay gammas. Then, the MENDEL evolution solver computes the decay photon sources for each region based on the neutron fluxes and/or the reaction rates calculated in the previous step, as well as the specified irradiation and cooling times. Finally, Tripoli-4® simulates the transport of the decay photons and computes the dose rates in each region of interest.